From Delphi to JavaScript Today: Reviving My Old CIH Project
Back in 2009, I wrote a little side project in Delphi. The idea? Implement the Cheapest Insertion Heuristic (CIH) — a constructive algorithm to approximate solutions to the Traveling Salesman Problem (TSP).
At the time, it was mostly a coding experiment, tucked away in a folder, and later uploaded here: CIH on GitHub.
Fast forward more than a decade, I thought: “Why not bring this old project back to life, but in the browser?” No installers, no legacy IDEs, just a simple vanilla JavaScript + canvas demo that anyone can click and play with.
👉 Demo: CIH-JS Visualization
What is CIH Anyway?
CIH stands for Cheapest Insertion Heuristic. It’s one of those “good enough, fast enough” strategies for tackling the classic Traveling Salesman Problem (TSP):
👉 Given a set of cities and distances between them, what’s the shortest route that visits each city exactly once and returns home?
Solving TSP exactly can be painfully slow, but CIH takes a more pragmatic approach:
- Start with a small tour (two connected nodes).
- Insert new nodes one by one.
- At each step, choose the insertion spot that increases the total distance the least.
It’s not guaranteed to be the absolute best route, but it’s often very close, and super fast.
Calculating Distances (Yes, That Formula From School)
Before the “heuristic magic,” we need the basics: measuring the distance between two nodes.
And here’s the joke: you already know this. Yep, it’s just the good old Pythagorean theorem. Remember sitting in class thinking, “When will I ever use this in real life?” Well… this is one of those times.
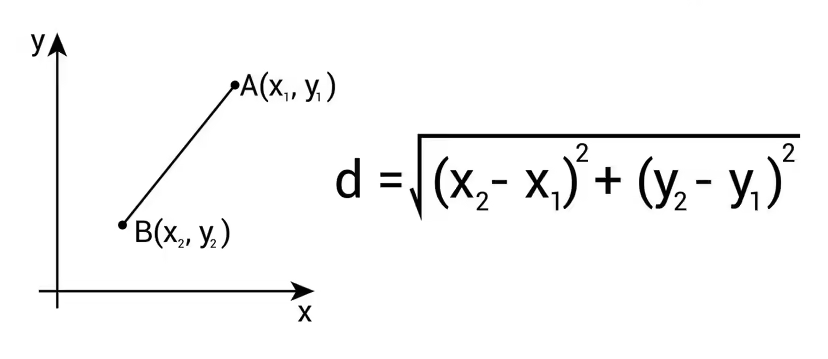
In code:
function calculateDistance(node1, node2) {
const dx = node2.x - node1.x;
const dy = node2.y - node1.y;
return Math.sqrt(dx * dx + dy * dy);
}
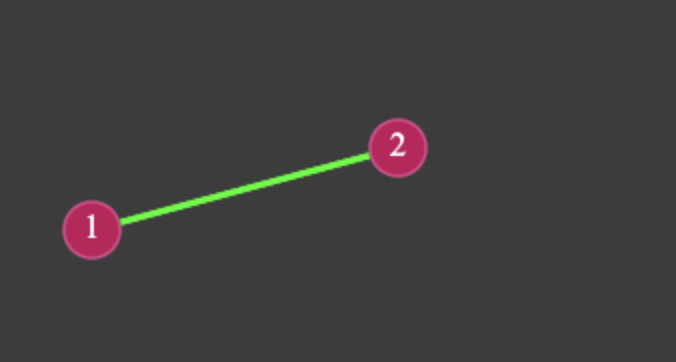
Here’s how it looks visually after adding two nodes:
Insertion Cost (Like Inviting a New Friend Into the Group Chat)
The essence of CIH is finding the cheapest place to add a new node into the tour.
Think of it like a group chat with your friends. A new buddy wants in. You don’t just drop them randomly — you place them where they’ll “fit in” without messing up the flow of conversation.
That’s what the algorithm does: it tests all possible spots and picks the least disruptive one.
function calculateInsertionCost(tour, newNodeId) {
let minCost = Infinity;
let bestInsertion = null;
for (let i = 0; i < tour.length; i++) {
const current = tour[i];
const distanceCurrent = getDistance(current.from, current.to);
const distanceNewFrom = getDistance(current.from, newNodeId);
const distanceNewTo = getDistance(newNodeId, current.to);
const insertionCost = distanceNewFrom + distanceNewTo - distanceCurrent;
if (insertionCost < minCost) {
minCost = insertionCost;
bestInsertion = { from: current.from, to: current.to, newNodeId };
}
}
return bestInsertion;
}
On the canvas, when a third node is added, the algorithm tries different positions before settling on the cheapest insertion:
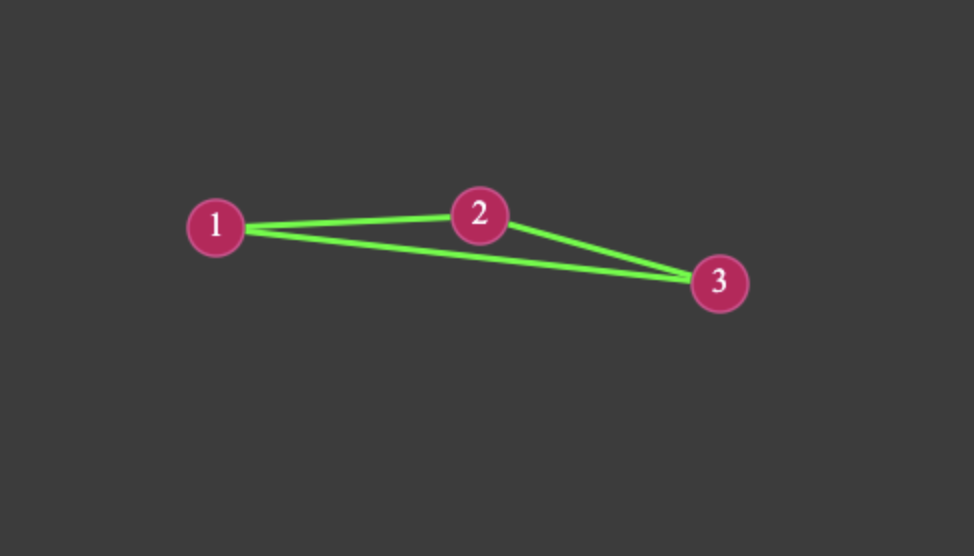
Visualizing the Tour
This is where the JavaScript port really shines:
- Click on the canvas → a new node is added.
- Distance table updates → showing all pairwise distances.
- Sub-tours are logged → step-by-step narration of how the algorithm chooses.
- Canvas highlights:
- All possible connections = light purple-gray.
- Current shortest path = bright green.
- Nodes = red circles with white IDs.
Here’s a shot after several nodes have been placed:
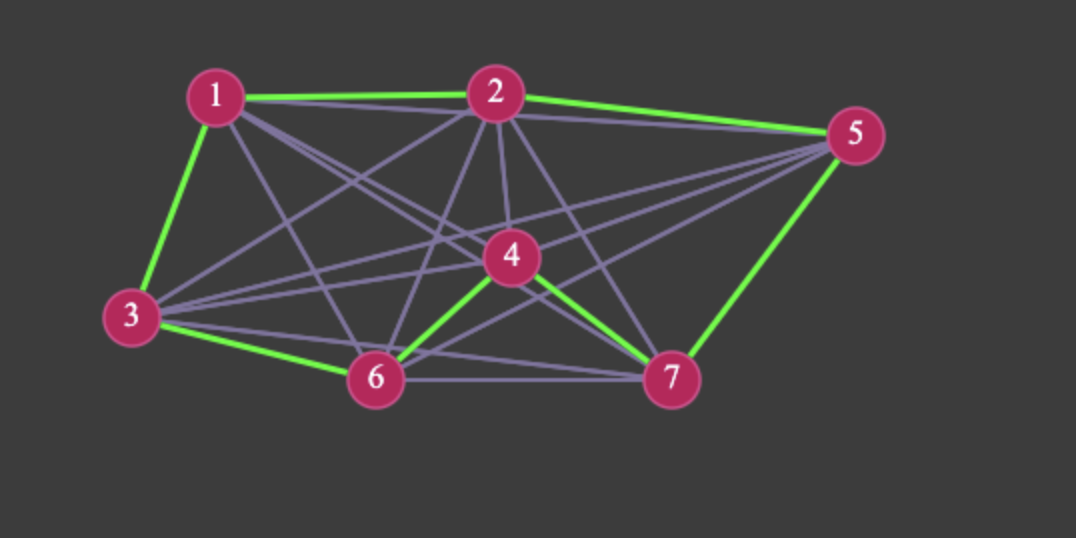
Notice the lime-green path? That’s the current “cheapest insertion” tour chosen by the algorithm.
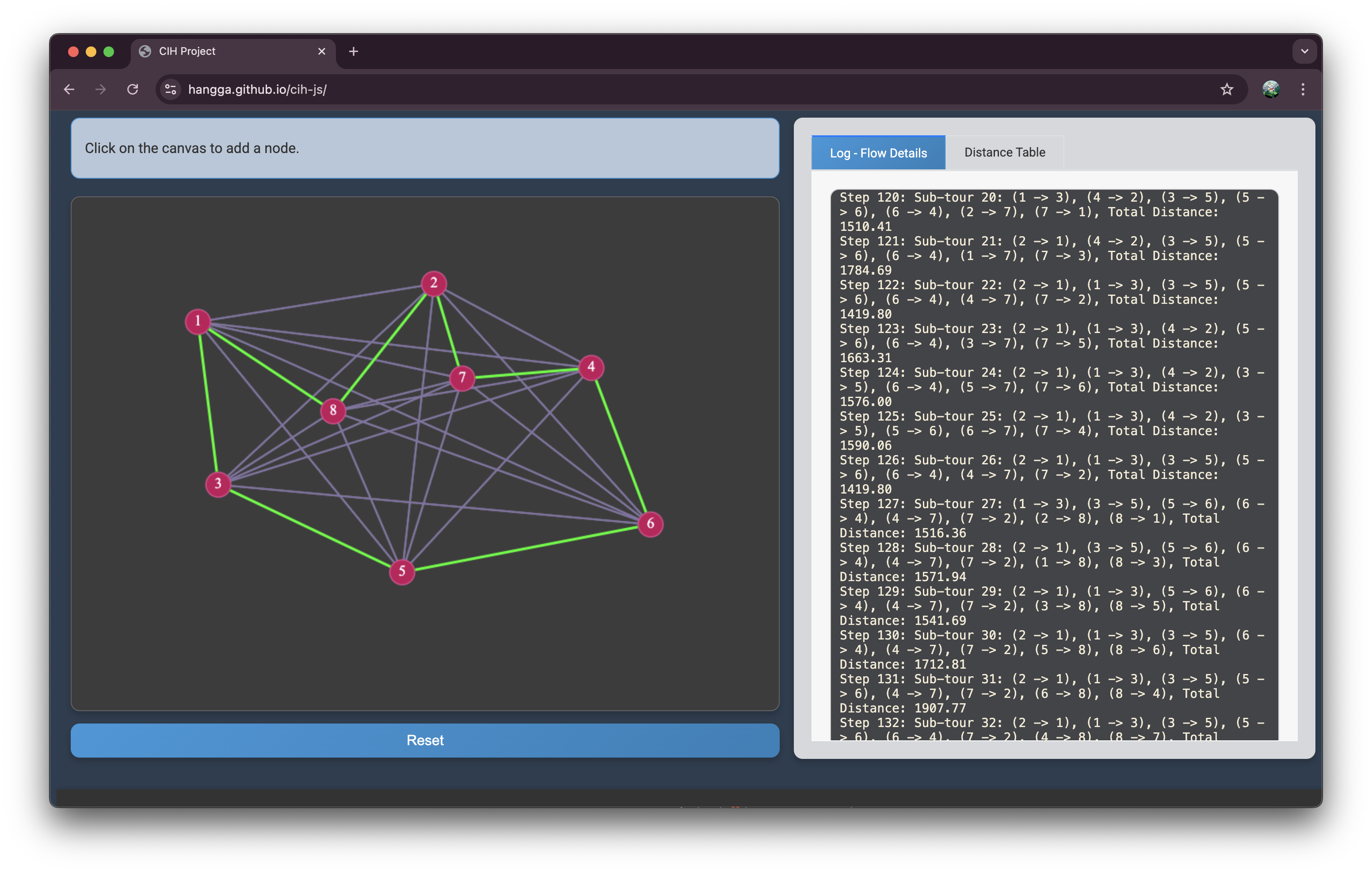
Log – Step-by-Step Flow
The log panel is basically a running commentary of how the CIH (Cheapest Insertion Heuristic) algorithm works behind the scenes.
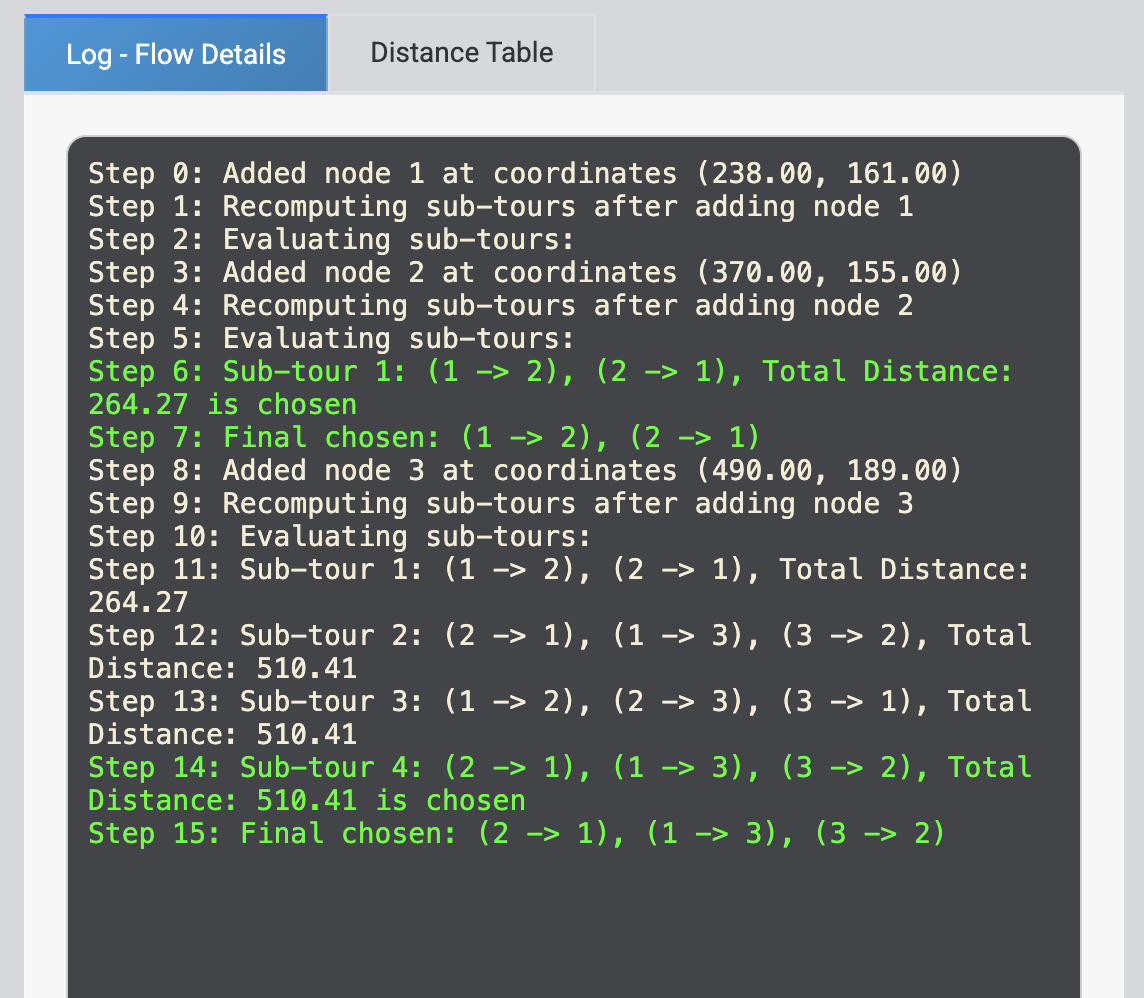
- Step 0–3 → Nodes are added with their coordinates (e.g., node 1 at
(238,161), node 2 at(370,155)). - Step 4–5 → The algorithm starts generating possible sub-tours.
- Step 6 → First sub-tour
(1 → 2), (2 → 1)with a total distance of 264.27. - Step 7 → That sub-tour is chosen as the temporary best route.
- Step 8–15 → A new node is inserted, insertion costs are calculated, and the cheapest option is picked.
- The final chosen route for 3 nodes becomes: (2 → 1), (1 → 3), (3 → 2) with a total of 510.41.
For a larger example (7 nodes, third screenshot):
- The algorithm generates multiple candidate sub-tours (Step 80–95), each with its own total distance.
Example:
- Step 83:
(2 → 1), (1 → 3), (3 → 4), (4 → 5), (5 → 2)→ 752.79 - Step 90:
(1 → 3), (4 → 5), (5 → 2), (3 → 6), (6 → 4), (2 → 7), (7 → 1)→ 1048.52
- Step 83:
- Step 96 → The sub-tour with total distance 820.10 is selected.
- Step 97 (Final chosen) → The final optimal tour:
(2 → 1), (1 → 3), (3 → 6), (6 → 4), (4 → 7), (7 → 5), (5 → 2)
with total distance 820.10.
👉 In short, the log shows the trial-and-error journey as the algorithm compares insertion options and narrows down to the shortest tour.
Distance Table
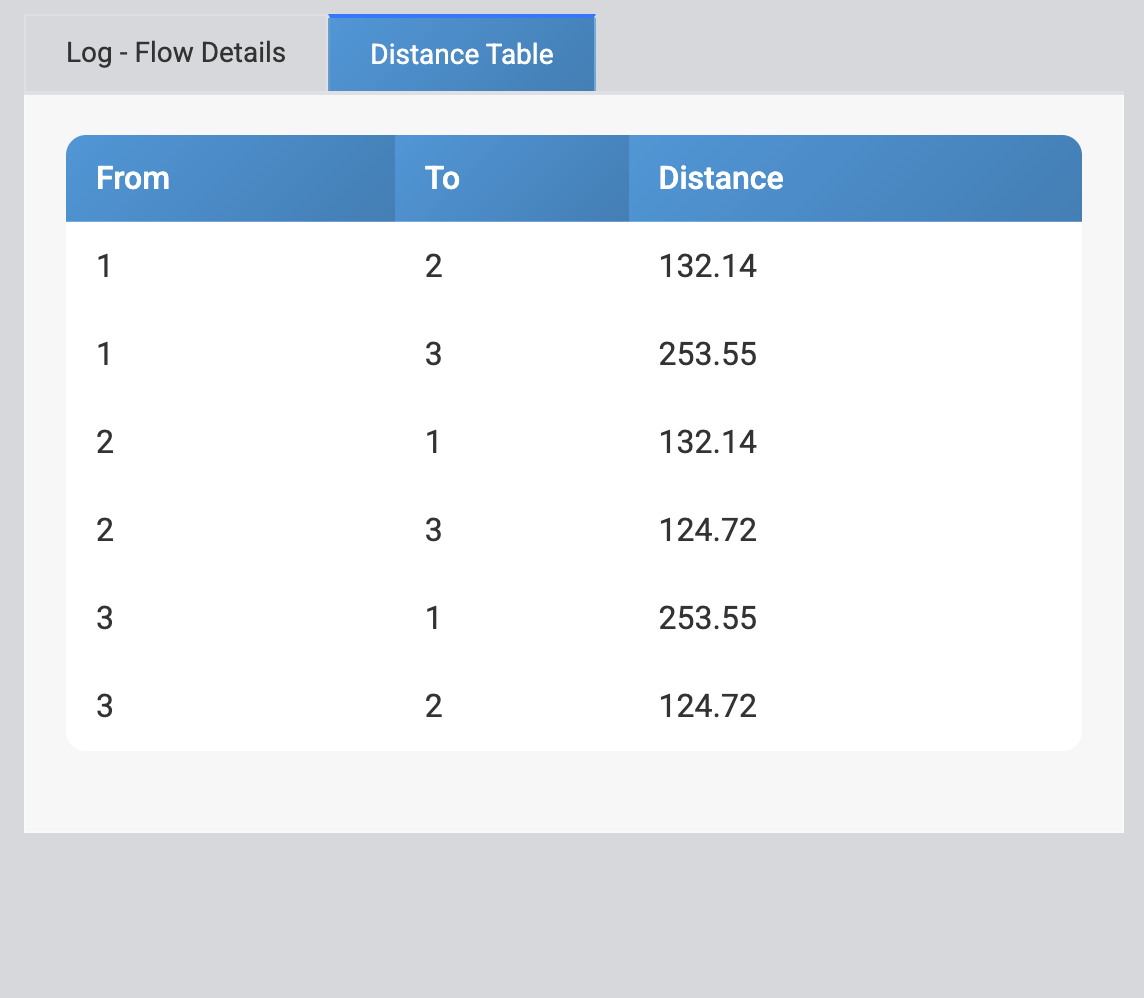
The distance table is the raw data behind all those calculations. It lists pairwise distances between every node.
Example:
- From 1 → 2 = 132.14
- From 2 → 3 = 124.72
- From 3 → 1 = 253.55
The CIH algorithm keeps referring back to this table to evaluate insertion costs and compute total route distances.
Takeaway
- The log = step-by-step narration of the CIH process.
- The distance table = the foundation data that powers those calculations.
- The final chosen route = the best tour selected with the shortest overall distance.
Looking Back, Moving Forward
What started as a Delphi project in 2009 has now been reimagined in JavaScript, complete with visual feedback and a friendlier explanation.
It’s a reminder that sometimes, old code doesn’t have to stay in the past — it can evolve, adapt, and even become more fun than before.
So if you’re curious about optimization, algorithms, or just want to see high school math doing something cool: give CIH a try.
👉 Live demo: CIH-JS
 Hangga Aji Sayekti
Hangga Aji Sayekti 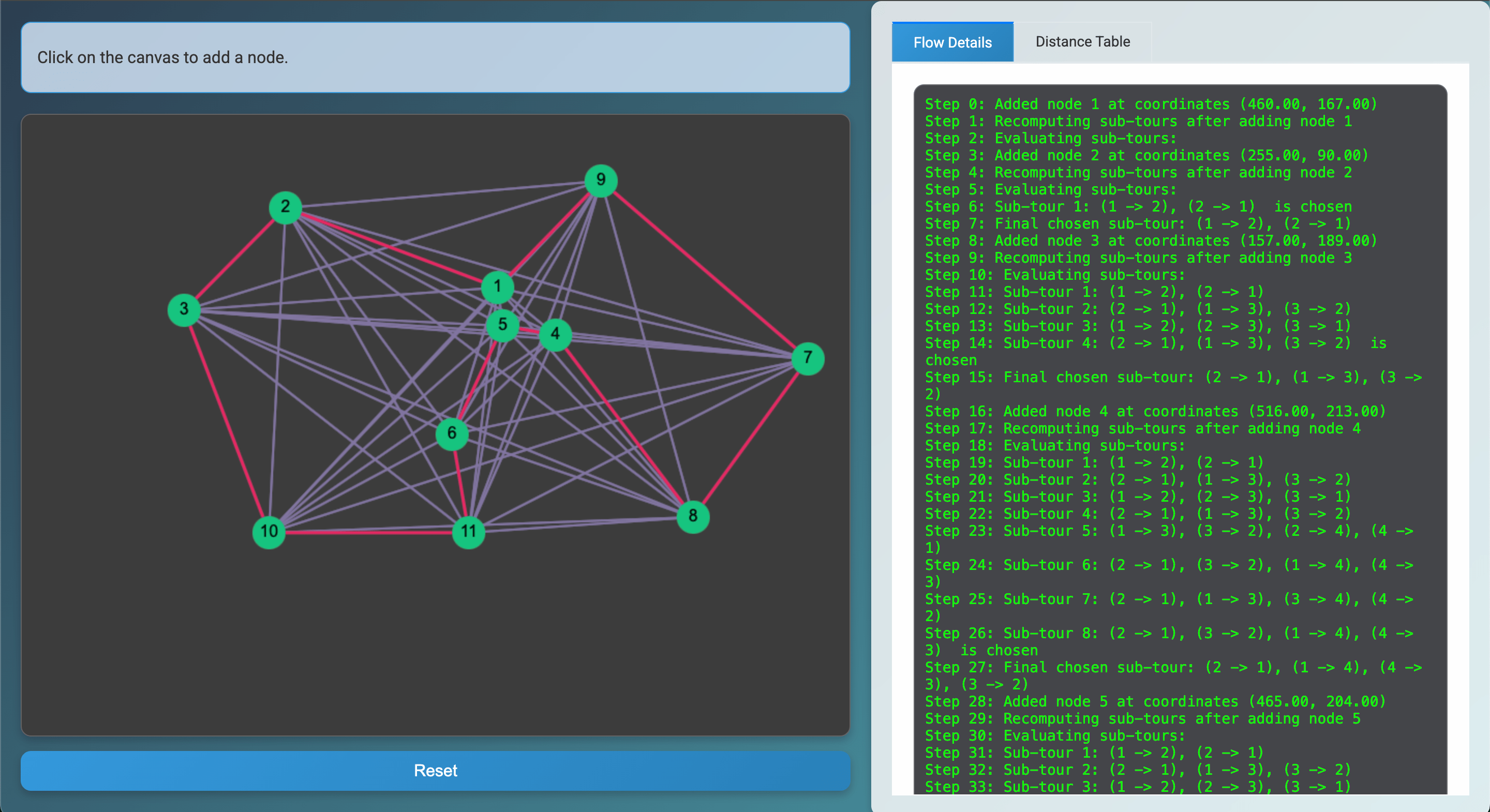
 Matplotlib : Visualisasi Sederhana Riwayat Hidup 4 Imam Madzhab
Matplotlib : Visualisasi Sederhana Riwayat Hidup 4 Imam Madzhab